Matematičar konačno riješio zagonetku kako unijeti trosjed u stan
Matematičar Jineon Baek sa Sveučilišta Yonsei u Južnoj Koreji objavio je stostranični dokaz koji rješava dugogodišnju matematičku zagonetku poznatu kao "problem useljenja trosjeda". Riječ je o izračunu najvećega dvodimenzionalnog predmeta koji se može provući kroz L-oblikovani hodnik.
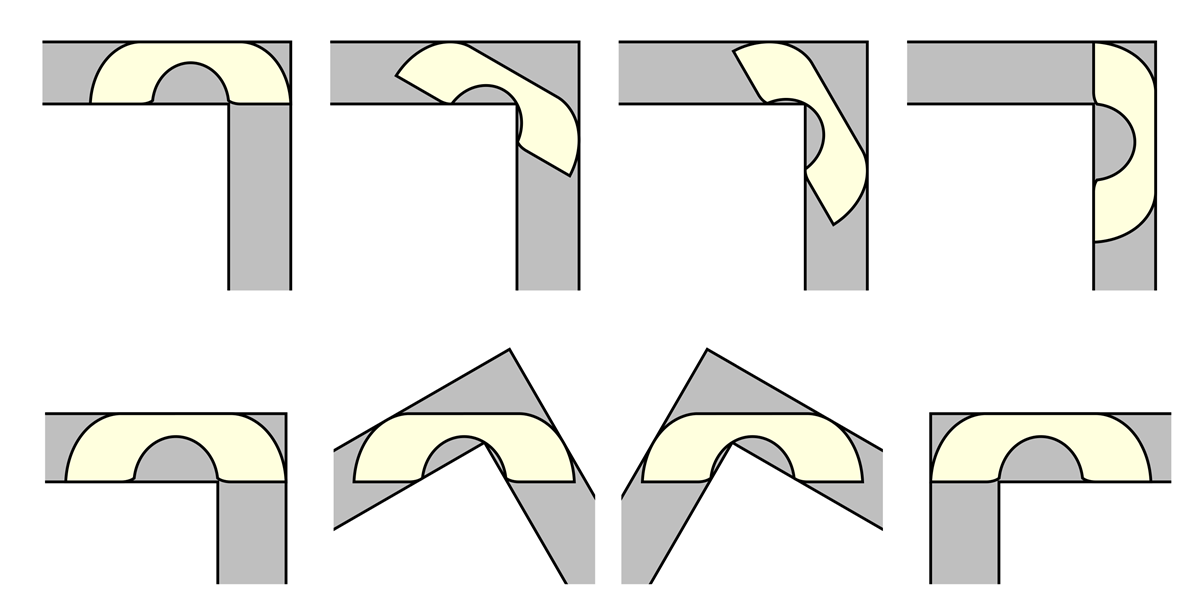
Problem "useljenja trosjeda" je 1966. godine formalno postavio austrijsko-kanadski matematičar Leo Moser. Za hodnik širine jedne jedinice, predmet kvadratnoga oblika površine jedne jedinice lako prolazi. Međutim, pravokutni predmet površine dvije jedinice neizbježno zapinje.

Britanski matematičar John Hammersley ponudio je 1968. godine prvo značajno rješenje. Njegov dizajn sofe, sastavljen od presječenoga polukruga odvojenoga kvadratom s polukružnim udubljenjem, imao je površinu od 2,2074 jedinice. Hammersley je također postavio gornju granicu – nijedan predmet veći od 2,8284 jedinice ne bi mogao proći.
Joseph Gerver sa Sveučilišta Rutgers unaprijedio je Hammersleyjev dizajn 1992. godine. Dodavanjem dodatnih lukova i zaobljavanjem rubova, stvorio je oblik površine nešto veće od 2,2195 jedinica. Gerver je dokazao da je njegovo rješenje optimalno unutar zadanih uvjeta.

Znanstvenici Yoav Kallus i Dan Romik su 2018. godine računalnom simulacijom pokazali teoretsku mogućnost sofe površine do 2,37 jedinica.
U svojem najnovijem dokazu, Baek je primijenio matematički koncept injektivne funkcije za mapiranje uspješnih oblika Gerverove sofe. Nakon proširenja kroz veće dimenzije, potvrdio je da je Gerverova površina od 2,2195 jedinica zaista maksimalna moguća za zadane uvjete hodnika.

Iako još nije prošao znanstvenu recenziju njegovih kolega, Baekov dokaz mogao bi biti konačna riječ o problemu sofe, barem za jednostavni L-oblikovani hodnik. Za složenije scenarije s dodatnim zavojima preporučuje se oblik poznat kao Romikova ambideksterna sofa.



























